5G-NR-PDSCH学习

发表于 | 分类于
字数统计: 4.8k | 阅读时长 ≈ 21
《你的名字》

1 PDSCH 物理流程

1.1 加扰

双码字传输时，$q \in {0,1}$；单码字传输时，$q = 0$。[TS 38.211 7.3.1.1]
每一个码字对应的原始数据 $b{(q)}(0),…,b{(q)}(M_{bit}^{(q)}-1)$ ,经过加扰处理生成加扰后的数据为 $\widetilde b^{(q)}(0),…,\widetilde b{(q)}(M_{bit}{(q)}-1)$ 。加扰处理如下所示：
$$
\widetilde b^{(q)}(i) = (b^{(q)}(i) + c^{(q)}(i))mod2
$$
加扰序列是一个伪随机序列，由[TS 38.211 5.2.1]给出，加扰序列的初始为：
$$
C_{init} = n_{RNTI}\cdot2{15}+q\cdot2{14}+n_{ID}
$$

其中：

  • $n_{ID}$ = dataScramblingIdentityPDSCH(如果配置)，并且RNTI = C-RNTI or CS-RNTI，在公共搜索空间中不使用DCI格式1_0调度传输。
  • 除此之外 $n_{ID} = N_{ID}^{cell}$
  • $n_{RNTI}$ 就是PDSCH当前传输时相关联的RNTI

1.2 调制

每一个码字加扰后的比特块 $\widetilde b^{(q)}(0),…,\widetilde b{(q)}(M_{bit}{(q)}-1)$ 采用下表中的一种调制方式进行调制，得到一个复值调制符号块$d{(q)}(0),…,d{(q)}(M_{symb}^{(q)}-1)$。[TS 38.211 7.3.1.2]

Modulation scheme
Modulation order
QPSK
2
16QAM
4
64QAM
6
256QAM
8

1.3 层映射

每一个码字生成的调制信号 $d{(q)}(0),…,d{(q)}(M_{symb}^{(q)}-1)$ 根据下表映射到多个层$x(i)=[x^0{i} \cdots x{v-1}(i)]T$，$i = 0,1,…,M_{symb}{layer}-1$，其中$v$表示层数，$M_{symb}{layer}$ 表示每层调制符号的数量。[TS 38.211 7.3.1.3]

层数码字数码字到层映射
$i = 0,1,…,M_{symb}^{layer}-1$
11$x^{(0)}(i) = d^{(0)}(i)$ $M_{symb}^{layer} = M_{symb}^{(0)}$
21$x^{(0)}(i) = d^{(0)}(2i)$
$x^{(1)}(i) = d^{(0)}(2i+1)$ $M_{symb}^{layer} = M_{symb}^{(0)}/2$
31$x^{(0)}(i) = d^{(0)}(3i)$
$x^{(1)}(i) = d^{(0)}(3i+1)$ $M_{symb}^{layer} = M_{symb}^{(0)}/3$
$x^{(2)}(i) = d^{(0)}(3i+2)$
41$x^{(0)}(i) = d^{(0)}(4i)$
$x^{(1)}(i) = d^{(0)}(4i+1)$
$x^{(2)}(i) = d^{(0)}(4i+2)$ $M_{symb}^{layer} = M_{symb}{(0)}/4$<br/>$x{(3)}(i) = d^{(0)}(4i+3)$
52$x^{(0)}(i) = d^{(0)}(2i)$
$x^{(1)}(i) = d^{(0)}(2i+1)$
$x^{(2)}(i) = d^{(1)}(3i)$ $M_{symb}^{layer} = M_{symb}^{(0)}/2 = M_{symb}{(1)}/3$<br/>$x{(3)}(i) = d{(1)}(3i+1)$<br/>$x{(4)}(i) = d^{(1)}(3i+2)$
62$x^{(0)}(i) = d^{(0)}(3i)$
$x^{(1)}(i) = d^{(0)}(3i+1)$
$x^{(2)}(i) = d{(0)}(3i+2)$<br/>$x{(3)}(i) = d^{(1)}(3i)$ $M_{symb}^{layer} = M_{symb}^{(0)}/3 = M_{symb}{(1)}/3$<br/>$x{(4)}(i) = d{(1)}(3i+1)$<br/>$x{(5)}(i) = d^{(1)}(3i+2)$
72$x^{(0)}(i) = d^{(0)}(3i)$
$x^{(1)}(i) = d^{(0)}(3i+1)$
$x^{(2)}(i) = d{(0)}(3i+2)$<br/>$x{(3)}(i) = d^{(1)}(4i)$ $M_{symb}^{layer} = M_{symb}^{(0)}/3 = M_{symb}{(1)}/4$<br/>$x{(4)}(i) = d{(1)}(4i+1)$<br/>$x{(5)}(i) = d{(1)}(4i+2)$<br/>$x{(6)}(i)=d^{(1)}(4i+3)$
82$x^{(0)}(i) = d^{(0)}(4i)$
$x^{(1)}(i) = d^{(0)}(4i+1)$
$x^{(2)}(i) = d{(0)}(4i+2)$<br/>$x{(3)}(i)=d{(0)}(4i+3)$<br/>$x{(4)}(i) = d^{(1)}(4i)$ $M_{symb}^{layer} = M_{symb}^{(0)}/4 = M_{symb}{(1)}/4$<br/>$x{(5)}(i) = d{(1)}(4i+1)$<br/>$x{(6)}(i) = d{(1)}(4i+2)$<br/>$x{(7)}(i)=d^{(1)}(4i+3)$

可以看到，单码字映射到1-4层，双码字映射到5-8层。

1.4 天线端口映射

经过层映射之后的数据按照如下方式映射到天线端口。[TS 38.211 7.3.1.4]
$$
\left[
\begin{matrix}
y^{(p_0)}(i)\
\vdots\
y^{(p_{v-1})}(i)\
\end{matrix}
\right]= \left[
\begin{matrix}
x^{(0)}(i)\
\vdots\
x^{(v-1)}(i)
\end{matrix}
\right]
$$

其中 $i=0,1,…,M_{symb}{ap}-1$，$M_{symb}{ap}=M_{symb}^{layer}$

1.5 映射到虚拟资源快

对于每个天线步骤，都会创建一个虚拟资源网格。在资源网格内，从RE的最低频率到较高频率的来自来填充PDSCH数据到每个RE中。一旦它以分配的PDSCH资源块的最高频率到达RE，则移至下一个OFDM符号的最低频率的RE。[TS 38.211 7.3.1.5]
但不应使用为以下目的而分配的RE：

  • 分配给与要发送的PDSCH相关的DMRS的RE
  • 为DMRS分配给用于其他共同调度UE的RE
  • 非零功率CSI-RS的RE，由MeasObjectNR IE中较高层参数CSI-RS-Resource-Mobility配置的非零功率CSI-RS除外。
  • PTRS的RE
  • 声明为“不适用于PDSCH的RE”

1.6 从虚拟资源块映射到物理资源块

从VRB到PRB的映射有交织和非交织两种。[TS 38.211 7.3.1.6]

1.6.1 非交织

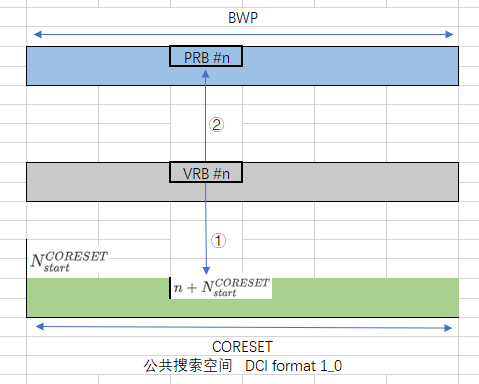
在公共搜索空间用DCI Format 1_0调度的PDSCH传输这种情况下,虚拟资源块$n$映射到物理资源块 $n + N_{start}^{CORESET}$ 上，其中$N_{start}^{CORESET}$是接受相应DCI的控制资源集中编号最小的物理资源块；
除此情况之外，虚拟资源块$n$就映射到物理资源块$n$上。
如下图所示：

1.6.2 交织

交织映射模式，以资源块束(RB bundle)来定义，与PDCCH的RB bundle 相比PDSCH的资源块束有些不同，主要分三种情况：
类型一：
在CORESET#0的Type0-PDCCH公共搜索空间，由SI-RNTI加扰，用DCI Format 1_0 调度的PDSCH传输。
下行初始激活的BWP，大小$N_{BWP,init}^{size}$，分为$N_{bundle} = \lceil N_{BWP,init}^{size}/L \rceil$ 个RB bundle，按照RB编号和束编号升序排序。其中$L$是bundle的大小，取值为２。如果$N_{BWP,init}^{size}$不能整数L，最后一个RB bundle包含 $N_{BWP,init}^{size}modL$个RB，其实由于$L = 2$所以最后一个不能整数的话那就剩下一个RB，能整数除最后一个RB bundle就是2个RB。
如下图所示：

类型二：
除上述情况外，在公共搜索空间由DCI Format 1_0调度的PDSCH传输。
BWP起始位置$N_{BWP,i}{start}$，大小为$N_{BWP,init}{size}$ 的VRB集合${0,1,…,N_{BWP,init}^{size}-1}$ 分为$N_{bundle}$ 个虚拟RB bundle，相应的$N_{BWP,init}^{size}$ 个PRB集合${N_{start}{CORESET},N_{start}{CORESET}+1,…,N_{start}{CORESET}+N_{BWP,init}{size}}$ 分为$N_{bundle}$ 个物理RB bundle，其中$N_{bundle}=\lceil (N_{BWP,init}{size}+(N_{BWP.i}{start}+N_{start}^{CORESET})modL)/L \rceil$ ，L是bundle的大小，取值为2，$N_{start}^{CORESET}$是接受相应DCI的控制资源集中编号最小的物理资源块。

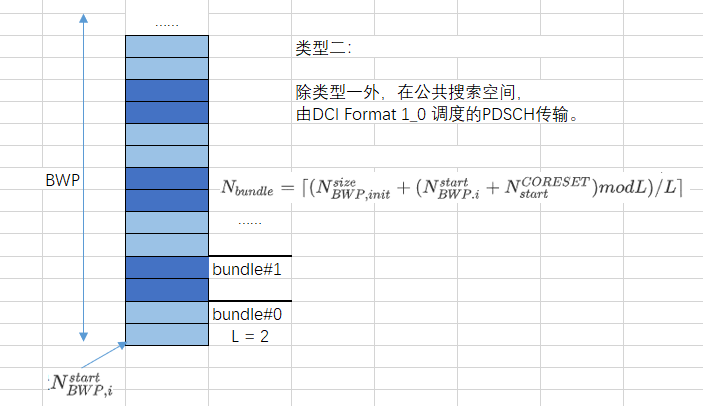
其RB bundle 包含的RB数如下描述：

  • 0号RB bundle 包含了$L-((N_{BWP,i}{start}+N_{start}{CONRESET})modL)$个RB；
  • 如果$(N_{BWP,init}{size}+N_{BWP,i}{start}+N_{start}^{CONRESET})modL>0$，则最后一个RB bundle包含了$(N_{BWP,init}{size}+N_{BWP,i}{start}+N_{start}^{CONRESET})modL$ 个RB，否则包含$L$个RB；
  • 其余RB bundle 包含$L$ 个RB；
    之所以要考虑进$N_{start}^{CONRESET}$，是因为38.214中规定，对于任何在PDCCH公共搜索空间中以DCI format 1_0调度的PDSCH传输，其RB编号从接受DCI的CORESET的最低RB开始。

类型三：
其他PDSCH传输。
BWP，i的起始位置$N_{BWP,i}{start}$，大小$N_{BWP,i}{size}$，分为$N_{bundle}$ 个RB bundle 且按照RB编号和束编号的升序排列，其中$N_bundle = \lceil(N_{BWP,init}{size}+(N_{BWP,i}{start}modL_i))/L_i \rceil$，$L_i$ 是bundle的大小，由高层参数vrb- ToPRB-Interleaver配置。

其RB bundle 包含的RB数如下描述：

  • 0号RB bundle包含了$L_i-(N_{BWP,i}^{start}modL_i)$个RB，目的是为了从下一个bundle开始，每个bundle的起始位置都是$L_i $的整数倍；
  • 如果$(N_{BWP,i}{start}+N_{BWP,i}{size})modL_i>0$，最后一个RB bundle包含了$(N_{BWP,i}{start}+N_{BWP,i}{size})modL_i$ 个RB，否则包含$L_i$ 个RB；
  • 其余RB bundle 包含$L_i$ 个RB。

举个例子来描述类型三：
例子：假设$N_{BWP,i}^{start} = 5,N_{BWP,i}^{size} = 21$

  1. $L_i=5$
    $N_{bundle} = \lceil(N_{BWP,init}{size}+(N_{BWP,i}{start}modL_i))/L_i \rceil = \lceil(21+(5mod5))/5 \rceil = 5$
    $N_{bundle,0} = L_i-(N_{BWP,i}^{start}modL_i) = 5-(5mod5) =5$
    $N_{bundle,end} = (N_{BWP,i}{start}+N_{BWP,i}{size})modL_i = (5+21)mod5 = 1$
    $N_{bundle,other} = L_i = 5$
    如下图所示：

  1. $L_i=4$
    $N_bundle = \lceil(N_{BWP,init}{size}+(N_{BWP,i}{start}modL_i))/L_i \rceil = \lceil(21+(5mod4))/4 \rceil = 6$
    $N_{bundle,0} = L_i-(N_{BWP,i}^{start}modL_i) = 4-(5mod4) =3$
    $N_{bundle,end} = (N_{BWP,i}{start}+N_{BWP,i}{size})modL_i = (5+21)mod4 = 2$
    $N_{bundle,other} = L_i = 4$
    如下图所示：

1.6.3 VRB bundle 到 PRB bundle 的映射

本节来看属于$j\in {0,1,…,N_{bundle}-1}$ 区间内的虚拟RB向物理RB的映射：

  • $N_bundle - 1$号虚拟RB bundle映射到$N_{bundle}-1$号物理RB bundle；
  • 其余$j\in {0,1,…,N_{bundle}-2}$ 的虚拟RB bundle 遵循$f(j)$ 函数映射到物理RB bundle
    $$
    f(j) = rC+c\j = cR+r\r = 0,1,…,R-1\c = 0,1,…,C-1\R = 2\C = \lfloor N_{bundle}/R \rfloor
    $$

举个例子说明，运用上面的例子数据:

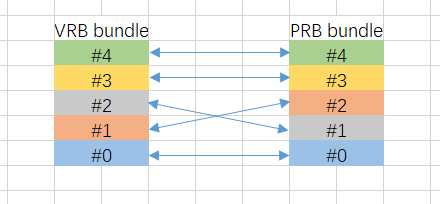
  1. $R = 2; \quad C = \lfloor N_{bundle}/R \rfloor = \lfloor 5/2 \rfloor = 2;\quad r = 0,1,2;\quad c = 0,1,2$。
crj: VRB bundle$f(j)$: PRB bundle
0000
0112
1021
1133

映射结果如图所示：

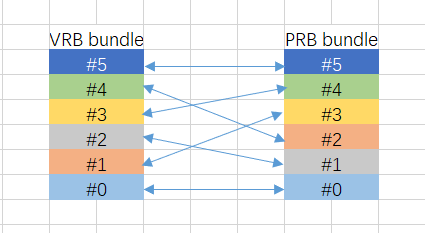
  1. $R = 2; \quad C = \lfloor N_{bundle}/R \rfloor = \lfloor 6/2 \rfloor = 3;\quad r = 0,1;\quad c = 0,1,2$。
crj: VRB bundle$f(j)$: PRB bundle
0000
0113
1021
1134
2042
2155

映射结果如下图所示：

2 PDSCH DMRS

2.1 序列生成

PDSCH DMRS序列有如下公式生成：
$$
r(n) = \frac{1}{\sqrt{2}}(1-2\cdot c(2n))+j\frac{1}{\sqrt{2}}(1-2\cdot c(2n+1))
$$
加扰序列采用31阶Gold序列生成，加扰序列的初始序列$c_{init}$如下式所示:
$$
c_{init} = (2{17}(N_{symb}{slot}n_{s,f}{\mu}+l+1)(2N_{ID}{n_{SCID}}+1)+2N_{ID}{n_{SCID}}+n_{SCID})mod2{31}
$$

其中：

  • $l$ 为时隙中的符号索引
  • $n_{s,f}$ 为时隙索引
  • $N_{symb}^{slot}$ 为一个时隙内的符号数量
  • $n_{SCID},N_{ID}^{n_{SCID}}$ :
    1) 对于C-RNTI/MCS-C-RNTI/CS-RNTI
    ① DCI format 1_1 , $n_{SCID}$ 可由DMRS-DownlinkConfig IE中scramblingID0,scramblingID1配置,可以在$N_{ID}0,N_{ID}1$之间选择,$N_{ID}{0},N_{ID}{1}\in {0,1,…,65535}$。
    ② DCI format 1_1 , $n_{SCID}$ 可由DMRS-DownlinkConfig IE中scramblingID0配置,可以在$N_{ID}0$之间选择,$N_{ID}{0}\in {0,1,…,65535}$。
    ③ 如果①DMRS-DownlinkConfig IE中scramblingID0,scramblingID1都未配置,则$n_{SCID}=0,N_{ID}{n_{SCID}}=N_{ID}{cell}$。
    ④ 如果②DMRS-DownlinkConfig IE中scramblingID0未配置，则$n_{SCID}=0,N_{ID}{n_{SCID}}=N_{ID}{cell}$。
    ２) 对于SI-RNTI/P-RNTI/RA-RNTI
    $n_{SCID}=0,N_{ID}{n_{SCID}}=N_{ID}{cell}$。

高层配置参数DMRS-DownlinkConfig内容如下：

2.2 PDSCH DMRS 频域位置

DMRS映射方式分为Configuration type 1 和configuration type 2 两种，有DMRS-DownlinkConfig中的drms-type指示，如果未配置，则默认为Configuration type 1。
序列映射到RE的公式如下所示：
$$
\alpha_{k,l}{p,\mu}=\beta_{PDSCH}{DMRS}w_f(k’)w_t(l’)r(2n+k’)\k = \begin{cases}4n+2k’+\Delta \quad \quad Configuration\quad type\quad1\6n+k’+\Delta\quad \quad Configuration\quad type\quad 2 \end{cases}\k’=0,1\l=\overline{l}+l’\n = 0,1,…
$$

$k$为频域指示，$l$为时域指示。Configuration type 1 和configuration type 2，分别用于支持单用户MIMO和多用户MIMO。除此之外，由于类型1和类型2平均每个端口占用的RE数量不同，即每个端口的RE密度不同，所以各自有不同的适用场景。类型1更适合低信噪比、频域选择性较高的场景，类型2更适合高信噪比、时延扩展较小的场景。

频域指示$k$的参考点分两种情况：

  • 承载SIB1的PDSCH的DMRS，$k$的参考点为CORESET#0的RE0；
  • 其余情况参考点为CRB#0的RE0即point A。

以下图示分别展示了Configuration type 1 和configuration type 2两种情况下的DMRS频域位置，为了方便只选取了1RB左右大小，都是single symbol。
Configuration type 1：

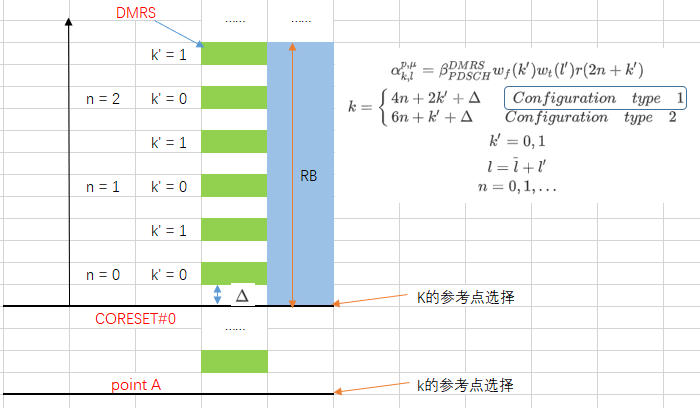
Configuration type 2:

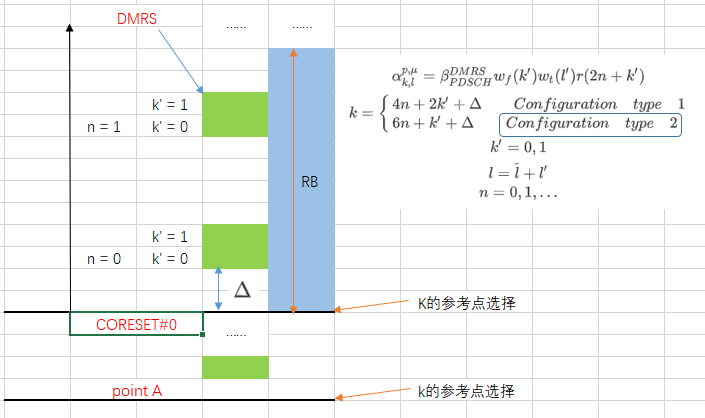
2.3 PDSCH DMRS 的符号位置

DMRS的符号位置取决于PDSCH的mapping type，分为mapping type A和mapping type B，参考表格或者配置可以获得PDSCH的mapping type，以及对应的$k_0,S,L$。[TS 38.214 5.1.2.1]



时域指示$l$的参考点分两种情况：

  • PDSCH mapping type A：时域指示$l$的参考点为时隙的起始symbol，且DM-RS的第一个符号位置为3或4(表中S = 2，3)，由MIB中参数dmrs-TypeA-Position指示，主要考虑PDCCH的具体配置。
  • PDSCH mapping type B时，$l$的参考点为PDSCH的起始symbol，DM-RS从PDSCH调度区域的第一个符号开始传输。
    两种情况如下图所示：
    例子一：type A，$S = 3 , L = 7$, $l_0$ 的大小是与参考点的差值，表示DMRS的初始符号。

例子二：type B，$S = 6 , L = 4$, $l_0$ 的大小是与参考点的差值，表示DMRS的初始符号。

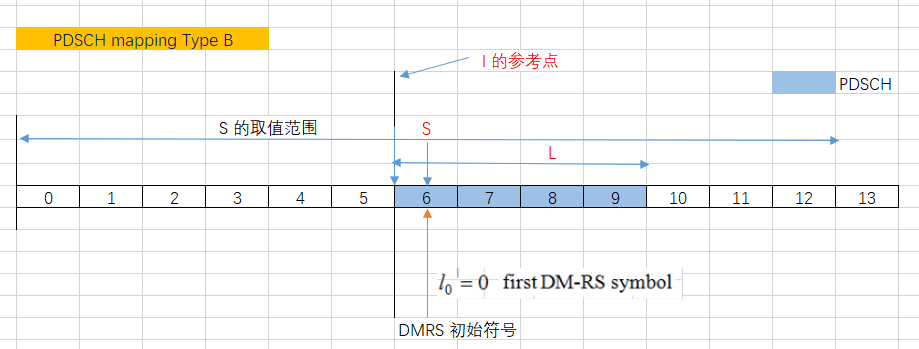
2.4 DMRS 符号类型

DMRS两个symbol类型，single symbol 和 double symbol。取决于DMRS-DownlinkConfig中的maxLength参数的配置，maxLength配置为len1，则取值为len1（single-symbol）；如果配置为len2（double-symbol）。如果高层参数maxLength没有配置，则为single类型。

2.5 添加导频

在NR中的中/高速场景中，为了保证估计精度，除了前置导频(前文所描述的DMRS)外，加入了与前置导频TDM的附加导频，附加DM-RS结构与前置DM-RS的图样相同，在double symbol DM-RS情况下，最多可以配置1组附加导频，在single symbol前置DM-RS情况下最多可以配置3组附加导频。附加导频的数量与调度时长有关，时域位置由高层参数dmrs-AdditionalPosition指示,如下表所示：

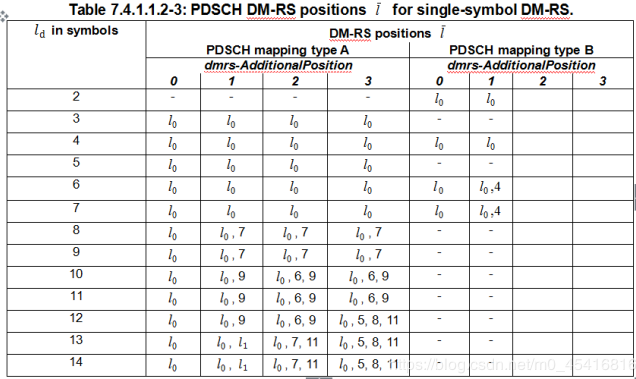
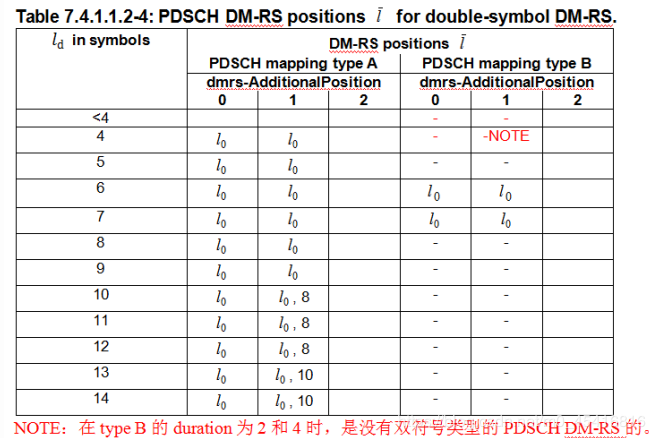
当PDSCH mapping type B时，如果PDSCH的资源和CORESET相重叠，则PDSCH DM-RS要往后顺延到紧挨CORESET的后面，此时，如果PDSCH的duration为2时，DM-RS的起始位置不能超过PDSCH的第二个symbol，当PDSCH的duration为4时，DM-RS的起始位置不能超过PDSCH的第3个symbol，当PDSCH的duration为7时，DM-RS的第一个symbol不能超过PDSCH的第4个symbol。
(Note: 以上所说的PDSCH的duration，也就是$L$，同时也是$l_d$ ，都是一个意思)

举个例子来说明上面两个表的意思：
$S = 2,L=11$,maxLength配置为len1，即为single symbol ,按照第一个 表格，如果此时$l_d = 11$ PDSCH mapping type A , dmrs-AdditionalPosition指示为2，则代表在DMRS导频位置分别在DMRS初始位置$l_0$(若为$l_0=2$),#6,#9符号上。如下图所示：

2.6 端口映射

结合PDSCH DMRS序列生成及映射公式，以及下表可知：

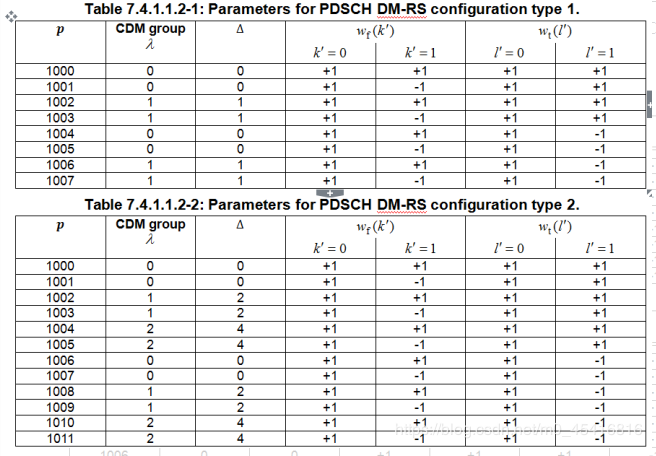
  • type 1，single symbol情况下，最多支持4个端口，端口0，1和2，3分别在不同的CDM group，每个CDM group内，比如端口0和1，又通过频域的OCC来实现正交，从而实现4个端口的正交。
  • type 1，double symbol情况下，最多支持8个端口，除了频域OCC外，还可以时域OCC来实现正交，所以可以支持更多的端口。
  • type 2，single symbol情况下，最多支持6个端口，共三个CDM group，每个group内又通过频域OCC实现正交。
  • type 2，double symbol情况下，最多支持12个端口，与类型1双符号情况同理，除了频域OCC外，还可以时域OCC，从而支持更多的端口。

问题：端口，层方面

3 PDSCH PTRS

3.1 相位噪声

相位噪声指射频器件在各种噪声（如随机性白噪声、闪烁噪声）的作用下引起的系统输出信号相位的随机变化。相位噪声会恶化接收端的SNR（Signal-Noise Ratio信噪比）或EVM（Error Vector Magnitude误差向量幅度），造成大量的误码，这样就限制了高阶调制的使用，会严重影响系统的容量。
相对来说，相位噪声对低频段，也就是sub6G频段的影响较小一些。而高频段（毫米波）下，由于参考时钟源的倍频次数大幅增加以及器件的工艺水平和功耗等各方面的原因，相位噪声的影响也是大幅增加。
为了应对高频段下的相位噪声，除了增大子载波间隔、提高器件质量之外，5G NR引入了PT-RS（Phase Tracking Reference Signal）信号以及相位估计补偿算法。

3.2 序列生成

生成序列方式与PDSCH DMRS相同。

3.3 高层配置

下行是否配置了PT-RS，由DMRS-DownlinkConfig中的字段phaseTrackingRS来决定，如果该字段缺省或配置为released，则表示下行没有PT-RS信号。PT-RS的具体配置在PTRS-DownlinkConfig中：

frequencyDensity
frequencyDensity提供了两个值，这两个值都在（1,276）的范围内，分别对应了[TS 38.214-Table5.1.6.3-2]中的$N_{RB0},N_{RB1}$，UE再通过DCI中的调度RB数查询该表，就可以确定PT-RS的频域密度$K_{PT−RSK}$ 。如果调度RB数过少，即$N_{RB}<N_{RB0}$ 时，PT-RS的系统开销相对来说就太大了，这个时候下行没有PT-RS信号。

scheduled bandwidthFrequency density ($K_{PT-RS}$)
$N_{RB}<N_{RB0}$PT-RS is not present
$N_{RB0}<N_{RB}<N_{RB1}$2
$N_{RB1}<N_{RB}$4

timeDensity
timeDensity提供了三个范围在（0,29）的值，分别对应[TS 38.214-Table5.1.6.3-1]中的ptrs-MCS1、ptrs-MCS2、ptrs-MCS3，UE再通过DCI中的调度MCS信息就可以确定PT-RS的时域密度(间隔)$L_{PT−RS}$，表中的ptrs-MCS4没有在高层参数中明确配置，UE可以假定该值为当前可使用的最大MCS+1。

scheduled MCSTime density ($L_{PT-RS}$)
$ptrs-MCS1\leq l_{MCS}<ptrs-MCS2$4
$ptrs-MCS2\leq l_{MCS}<ptrs-MCS3$2
$ptrs-MCS3\leq l_{MCS}<ptrs-MCS4$1

epre-Ratio
epre-Ratio通过[TS 38.214-Table4.1-2] 确定了PT-RS端口每层每个RE上PT-RS EPRE与PDSCH EPRE的比例，这个比例叫$\rho {PTRS}$, 它与$\beta{PTRS}$ 的关系为：$\beta_{PTRS}=10^{\frac {\rho_{PTRS}}{20}}$。

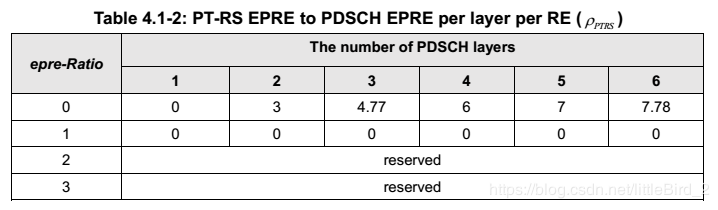
resourceElementOffset 见下文表格中参数，取值为{00,01,10,11}。

3.4 资源映射

如果PTRS存在，UE将按照按$\beta_{PT_RS}$缩放，并映射到资源单元中：
$$
\alpha_{k,l}^{p,\mu} = \beta_{PT-RS}\cdot r_k
$$

3.4.1 时域索引

确定时域索引$l$的步骤如下：

1
2
3
4
5
6
7
set i = 0 and l_{ref}=0  
if l_{ref}+iL_{PTRS}  overlaps with a symbol used for DM-RS according to clause 7.4.1.1.2
- set i = 1 
- set l_{ref} to the number of the last DM-RS symbol in a sequence of time-contiguous DM-RS occasions
add l_{ref} + iL_{PTRS} to the set of time indices for PT-RS
increment  i by one
repeat from step 2 above as long as l_{ref}+iL_{PTRS} is inside the PDSCH allocation

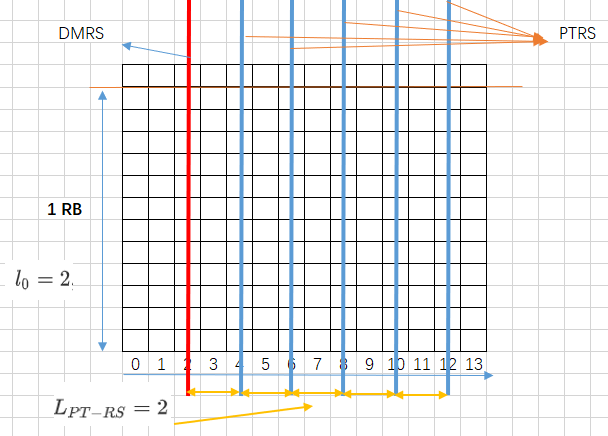
简而言之，PT-RS时域的的范围，从调度的PDSCH的第一个符号开始，避开DMRS所在的位置，以$L_{PT−RS}$为间隔，一直到PDSCH结束。$L_{PT-RS}$不仅是PT-RS之间的间隔，还是与DMRS最后一个符号之间的间隔。如下图所示：
图中 仅选取了$1 RB*14 symbol$ 资源单元 ， $l_0 = 2 , L_{PT-RS} = 2$ , single symbol类型。

3.4.2 频域索引

首先，假定分配给PDSCH的RB为从0到$N_{RB}-1$，那么分配给PDSCH的子载波范围就是0-$N_{sc}^{RB}N_{RB}-1$。最终PTRS频域索引$k$，由下面公式得到：
$$
k=k_{ref}{RE}+(iK_{PT-RS}+k_{ref}{RB})N_{sc}{RB}\k_{ref}{RB}= \begin{cases}n_{RNTI}modK_{PT-RS} \quad \quad \quad if N_{RB}modK_{PT-RS} = 0 \n_{RNTI}mod(N_{RB}modK_{PT-RS})\quad \quad otherwise\end{cases}
$$

$k_{ref}^{RE}$ 由下表获得[TS 38.311-Table 7.4.1.2.2-1]：

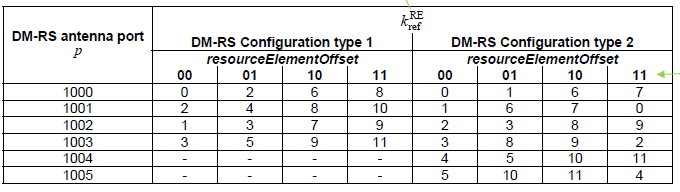
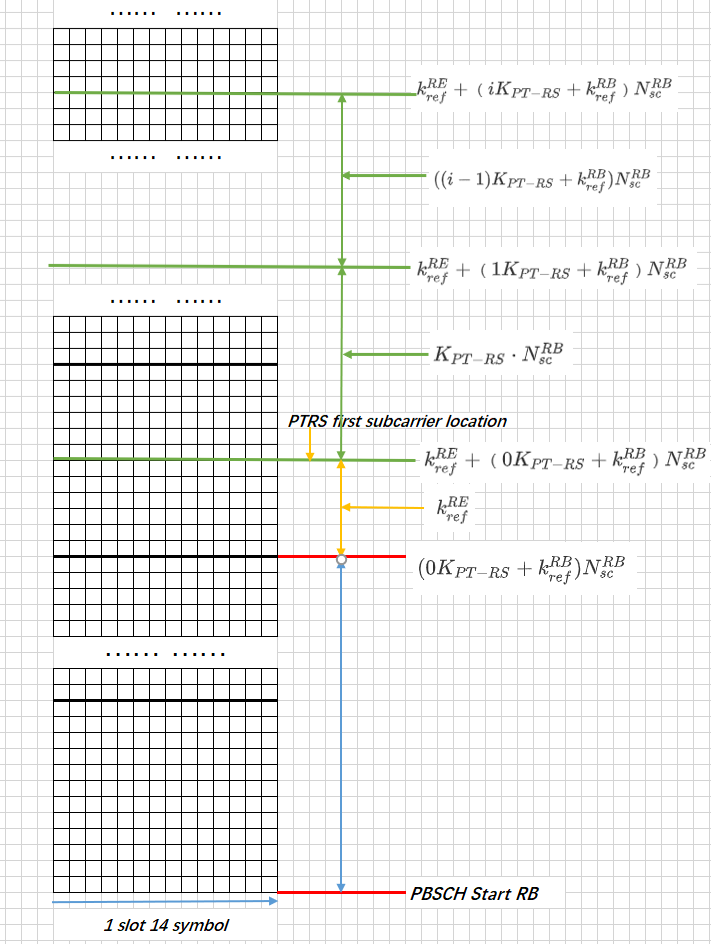
由上可知，$K_{PT-RS}$为相邻 PTRS之间间隔的RB数，即相邻 PTRS之间相差$K_{PT-RS}\cdot N_{sc}^{RB}$ 个子载波，第一个PTRS 子载波定位是 $k_{ref}{RE}+（0K_{PT-RS}+k_{ref}{RB}）N_{sc}^{RB}$ 。大概的图样如下图所示：

主要参考：
博客：https://blog.csdn.net/littleBird_2/article/details/89408575 (PDSCH)
博客：https://blog.csdn.net/kakamilan/article/details/104535554 (PDSCH-DMRS)
博客：https://blog.csdn.net/m0_45416816/article/details/103807853 (PDSCH-DMRS)
博客：https://blog.csdn.net/littleBird_2/article/details/89683712 (PDSCH-PTRS)
网页：http://www.sharetechnote.com



----------- 本文结束 -----------




0%