剑指offer -- 搜索与回溯算法

发表于 | 分类于
字数统计: 8k | 阅读时长 ≈ 37
沃特福德 -- 爱尔兰

剑指offer – 搜索与回溯算法

剑指 Offer 12. 矩阵中的路径

Difficulty: 中等

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

示例 1：

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

1
2
输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

  • 1 <= board.length <= 200
  • 1 <= board[i].length <= 200
  • board 和 word 仅由大小写英文字母组成

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int m = 0, n = 0;
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size();
        n = board[0].size();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (verify(board, word, i, j, 0)) return true;
            }
        }
        return false;
    }
    
    bool verify(vector<vector<char>>& board, string& word, int i, int j, int k) {
        // 超出边界的话直接返回 false
        if (i < 0 || i >= m || j < 0 || j >= n || board[i][j] != word[k]) return false;
        // 如果遍历到恰好长度，且元素相符合则返回 true
        if (k == word.size() - 1) return true;
        // 代表已经访问过，随便一个非字母的字符即可
        board[i][j] = '0';
        // 向四个方向进行搜索，只要有一方找到即可
        bool res = verify(board, word, i + 1, j, k + 1) || 
                   verify(board, word, i, j + 1, k + 1) ||
                   verify(board, word, i - 1, j, k + 1) ||
                   verify(board, word, i, j - 1, k + 1);
        // 回溯时候填回数字
        board[i][j] = word[k];
        return res;
    }
};

时间复杂度： $O(3^KMN)$ ， 最差情况下，需要遍历矩阵中长度为 K 字符串的所有方案，时间复杂度为 $O(3^K)$；矩阵中共有 $MN $ 个起点，时间复杂度为 $O(MN)$。

  • 方案数计算： 设字符串长度为 KK ，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下 3 种选择，因此方案数的复杂度为 $O(3^K)$。

空间复杂度： $O(K)$， 搜索过程中的递归深度不超过 K ，因此系统因函数调用累计使用的栈空间占用 $O(K)$（因为函数返回后，系统调用的栈空间会释放）。最坏情况下 $K = MNK=MN$ ，递归深度为 $MN$ ，此时系统栈使用 $O(MN)$ 的额外空间。

剑指 Offer 13. 机器人的运动范围

Difficulty: 中等

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

1
2
输入：m = 2, n = 3, k = 1
输出：3

示例 2：

1
2
输入：m = 3, n = 1, k = 0
输出：1

提示：

  • 1 <= n,m <= 100
  • 0 <= k <= 20

Solution

方法一：DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int movingCount(int m, int n, int k) {
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        return dfs(0, 0, 0, 0, visited, m, n, k);
    }
    int dfs(int i, int j, int si, int sj, vector<vector<bool>>& visited, int m, int n, int k) {
        // 如果越界，或者不满足数位大小之和，或者已经被访问过，则返回 0
        if (i >= m || j >= n || k < si + sj || visited[i][j] == 1) return 0;
        // 访问该点
        visited[i][j] = true;
                
        int a = (i + 1) % 10 ? si + 1 : si - 8;
        int b = (j + 1) % 10 ? sj + 1 : sj - 8;
        
        // 关于以上代码的一个简单的例子, 
        // 其中的 si 是当前横坐标各位之和, s_(i+1) 是下移后情况下横坐标各位之和
        // 19 -> 20  si = 10, s_(i+1) = 2, s_(i+1) = si - 8;
        // 18 -> 19  si = 9, s_(i+1) = 10, s_(i+1) = si + 1;
        
                   
        return 1 + dfs(i + 1, j, a, sj, visited, m, n, k)   // 下移
                 + dfs(i, j + 1, si, b, visited, m, n, k);  // 右移
                  
    }
};

方法二：BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int movingCount(int m, int n, int k) {
        vector<vector<bool>> visited(m, vector<bool>(n, 0));
        int res = 0;
        // 每次 push 是一个 四元组
        queue<vector<int>> q;
        q.push({0, 0, 0, 0});
        while (!q.empty()) {
            vector<int> x = q.front();
            q.pop();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if (i >= m || j >= n || k < si + sj || visited[i][j]) continue;
            visited[i][j] = true;
            res++;
            q.push({i + 1, j, (i + 1) % 10 ? si + 1: si - 8, sj});
            q.push({i, j + 1, si, (j + 1) % 10 ? sj + 1: sj - 8});
        }
        return res;
    }
};

两种方法时间复杂度，空间复杂度分析相同。

时间复杂度： $O(MN)$ ，最差情况下，机器人遍历矩阵所有单元格，此时时间复杂度为 $O(MN)$ 。
空间复杂度： $O(MN)$， 最差情况下，访问矩阵存储所有单元格的索引，使用 $O(MN)$ 的额外空间。

剑指 Offer 26. 树的子结构

Difficulty: 中等

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

1
2
3
4
5
    3  
   / \  
  4   5  
 / \  
1   2

给定的树 B：

1
2
3
  4   
 /  
1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

1
2
输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

1
2
输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        // true 条件：1. A B 都不为空
        // 2. A 是根节点，B为其子树; B 为 A 左（右）子树中的子树
        return (A && B) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
    bool recur(TreeNode* A, TreeNode* B) {
        // B 空则说明到底，期间没有错误，所以正确
        if (!B) return true;
        // A 空则说明，B 没有搜索到，或者 期间搜索错误，都说明搜索错误
        if (!A || A->val != B->val) return false;
        // 左子树对应左子树，右子树对应右子树
        return recur(A->left, B->left) && recur(A->right, B->right);
    }
};

时间复杂度：$O(MN)$， 其中 M, NM,N 分别为树 A 和 树 B 的节点数量；先序遍历树 A 占用 $O(M)$ ，每次调用 recur(A, B) 判断占用 $O(N)$ 。
空间复杂度： $O(M)$ ， 当树 A 和树 B 都退化为链表时，递归调用深度最大。当 $M≤N$ 时，遍历树 A 与递归判断的总递归深度为 M ；当 $M>N$ 时，最差情况为遍历至树 A 的叶节点，此时总递归深度为 M。

剑指 Offer 27. 二叉树的镜像

Difficulty: 简单

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

1
2
3
4
5
     4  
   /   \  
  2     7  
 / \   / \  
1   3 6   9

镜像输出：

1
2
3
4
5
     4  
   /   \  
  7     2  
 / \   / \  
9   6 3   1

示例 1：

1
2
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

限制：

0 <= 节点个数 <= 1000

Solution

方法一：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 写法一
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return nullptr;
        swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

// 写法二
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        return dfs(root);
    }
    TreeNode* dfs(TreeNode* root) {
        if (!root) return nullptr;
        TreeNode* node = new TreeNode(root->val);
        node->left = dfs(root->right);
        node->right = dfs(root->left);
        return node;
    }
};

时间复杂度：$O(N)$， 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点。
空间复杂度：$O(N)$， 最差情况下（当二叉树退化为链表），递归时系统需使用 $O(N)$ 大小的栈空间。

方法二：迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return nullptr;
        stack<TreeNode*> stk;
        stk.push(root);
        while (!stk.empty()) {
            TreeNode* node = stk.top();
            stk.pop();
            swap(node->left, node->right);
            if (node->right) stk.push(node->right);
            if (node->left) stk.push(node->left);
        }
        return root;
    }
};

时间复杂度：$O(N)$， 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点。
空间复杂度：$O(N) $， 最差情况下，栈 stack 最多同时存储 $\frac{N + 1}{2}$ ，占用 $O(N)$ 额外空间。

剑指 Offer 28. 对称的二叉树

Difficulty: 简单

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
    1  
   / \  
  2   2  
 / \ / \  
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
  1  
 / \  
2   2  
 \   \  
 3    3

示例 1：

1
2
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

1
2
输入：root = [1,2,2,null,3,null,3]
输出：false

限制：

0 <= 节点个数 <= 1000

Solution

方法一：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        return judge(root->left, root->right);
    }
    bool judge(TreeNode* l, TreeNode* r) {
        // 如果两个节点皆为空，返回 true
        if (!l && !r) return true;
        // 一个节点为空，另一个节点非空，返回 false
        else if (!l || !r) return false;
    	// 数值不同，返回 false
        else if (l->val != r->val) return false;
        return judge(l->left, r->right) && judge(l->right, r->left);
    }  
};

时间复杂度：$O(N)$，其中 N 为二叉树的节点数量，每次执行 judge() 可以判断一对节点是否对称，因此最多调用 N*/2 次 judge() 方法。
空间复杂度：$O(N)$， 最差情况下（当二叉树退化为链表），递归时系统需使用 $O(N)$ 大小的栈空间。

方法二：迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if  (!root) return true;
        queue<TreeNode*> q;
        q.push(root->left);
        q.push(root->right);
        while (!q.empty()) {
            TreeNode* u = q.front();
            q.pop();
            TreeNode* v = q.front();
            q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;
            q.push(u->left);
            q.push(v->right);
            q.push(u->right);
            q.push(v->left);
        }
        return true;
    }
};

时间复杂度：$O(N)$， 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点。
空间复杂度：$O(N) $， 这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 $O(N) $

剑指 Offer 32 - I. 从上到下打印二叉树

Difficulty: 中等

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回：

1
[3,9,20,15,7]

提示：

  1. 节点总数 <= 1000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        if (!root) return {};
        vector<int> res;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();
                res.push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return res;
    }
};

剑指 Offer 32 - II. 从上到下打印二叉树 II

Difficulty: 简单

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

提示：

  1. 节点总数 <= 1000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if (!root) return {};
        vector<vector<int>> res;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int size = q.size();
            vector<int> path;
            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();
                path.push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            res.push_back(path);
        }
        return res;
    }
};

剑指 Offer 32 - III. 从上到下打印二叉树 III

Difficulty: 中等

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

提示：

  1. 节点总数 <= 1000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (!root) return res;
        queue<TreeNode*> q;
        q.push(root);
        int level = 0;
        while (!q.empty()) {
            int size = q.size();
            level++;
            vector<int> path;
            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();
                path.push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            if (level % 2 == 0)
                reverse(path.begin(), path.end());
            res.push_back(path);
        }
        return res;
    }
};

剑指offer32 3 道题目时间空间复杂度分析相同

时间复杂度： $O(N)$， N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 ：$O(N)$，最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 $O(N)$ 大小的额外空间。

剑指 Offer 34. 二叉树中和为某一值的路径

Difficulty: 中等

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 target = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

返回:

1
2
3
4
[
   [5,4,11,2],
   [5,8,4,5]
]

提示：

  1. 节点总数 <= 10000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<int> path;
        dfs(root, sum, path);
        return res;
    }
    vector<vector<int>> res;
    void dfs(TreeNode* root, int sum, vector<int>& path) {
        if (!root) return;
        // 只要 root 非空
        path.push_back(root->val);
        sum -= root->val;
        // 如果处理该节点后满足 sum 条件，且是叶子节点，则找到一个数值
        if (sum == 0 && !root->left && !root->right) {
            res.push_back(path);
        }
        dfs(root->left, sum, path);
        dfs(root->right, sum, path);
        path.pop_back();
    }
};

时间复杂度：$O(N)$， 其中 N 为二叉树的节点数量，需要遍历树的所有节点。
空间复杂度：$O(N)$， 最差情况下（当二叉树退化为链表），path 存储所有节点，使用额外 $O(N)$ 空间

剑指 Offer 36. 二叉搜索树与双向链表

Difficulty: 中等

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

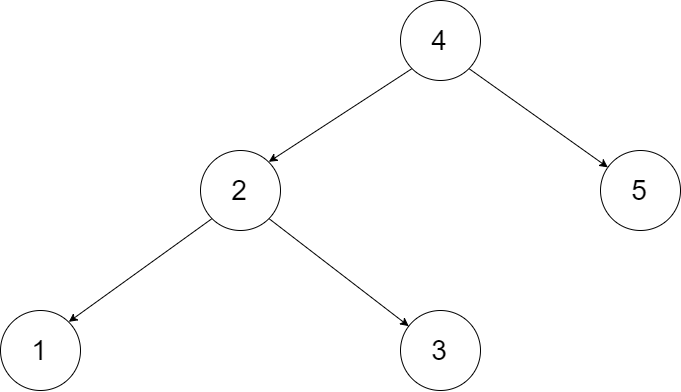
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

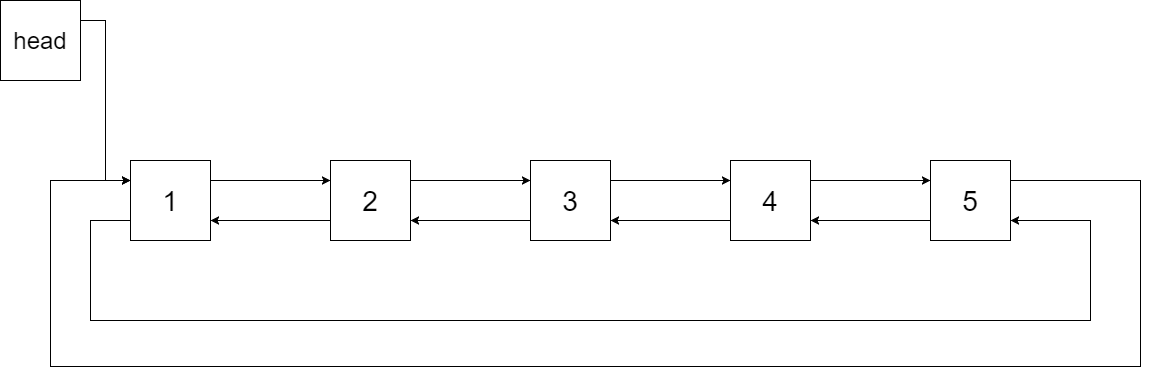
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if (!root) return nullptr;
        recur(root);
        // 首尾相连 :  pre <-- head,   pre --> head;
        head->left = pre;
        pre->right = head;
        return head;
    }
    Node* pre, head;
    //  中序遍历
    void recur(Node* cur) {
        if (!cur) return;
        recur(cur->left);
        
        // 前向存在，则 pre 右为 cur : pre  --> cur
        if (pre) pre->right = cur;
        // 否则说明当前 cur 为中序遍历最左侧子节点，也即是 head
        else head = cur;
        // 确定 cur 的左连接为 pre :  pre <-- cur
        cur->left = pre;
        // pre 向后遍历
        pre = cur;
        
        recur(cur->right);
    }
}；

时间复杂度：$O(N)$， 其中 N 为二叉树的节点数量，需要遍历树的所有节点。
空间复杂度：$O(N)$， 最差情况下（当二叉树退化为链表），递归深度 N，使用系统 $O(N)$ 栈空间。

剑指 Offer 37. 序列化二叉树

Difficulty: 困难

请实现两个函数，分别用来序列化和反序列化二叉树。

**示例: **

1
2
3
4
5
6
7
8
9
你可以将以下二叉树：

    1
   / \
  2   3
     / \
    4   5

序列化为 "[1,2,3,null,null,4,5]"

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        // 如果根节点为空则说明返回 "[]"
        // 层次遍历方法
        if (!root) return "[]";
        queue<TreeNode*> que;
        que.push(root);
        // 初始化先键入 [
        string data{"["};
        while (!que.empty()) {
            TreeNode* node = que.front();
            que.pop();
            // 如果当前节点存在的话
            if(node) {
                // 键入 val,
                data.append(to_string(node->val));
                data.append(",");
                // 键入 左右节点，是否为空不用判断
                que.push(node->left);
                que.push(node->right);
            } else {
                // 如果为空，输入 null, 即可
                data.append("null,");
            }
        }
        // 找到最后是数字的位置
        size_t post = data.find_last_of("0123456789");
        // 截取所需字符，也就是去除多添加的 null,
        data = data.substr(0, post + 1);
        // 末尾添加 ]
        data.append("]");
        return data;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        // 如果接受的字符串为 [] 则说明为空
        if(data == "[]") return nullptr;
        // 去 "[ ]"
        size_t len = data.size();
        data = data.substr(1, len - 2);
        // 提取 data 中所需的字符，也即是去除 ','
        // 所需字符存于 vector<string> 中
        vector<string> vec;
        // 用于记录中间变量
        string temp;
        for (int i = 0; i < data.size(); ++i) {
            // 遇到 ',' 则存入一次 string
            if (data[i] == ',') {
                vec.push_back(temp);
                temp = "";
            // 到达末尾，也进行存入 string 操作
            } else if (i == data.size() - 1) {
                temp += data[i];
                vec.push_back(temp);
                temp = "";
            // 除此之外，只要更新 string 即可
            } else {
                temp += data[i];
            }
        }
        // 首先现根据 vec[0] 创建根节点
        TreeNode* root = new TreeNode(stoi(vec[0]));
        queue<TreeNode*> que;
        que.push(root);
        int i = 1;
        while (!que.empty()) {
            // 如果 null 的话会逐渐的被 pop 出
            TreeNode* node = que.front();
            que.pop();
            // 不是 null，先创建左节点
            if (i < vec.size() && vec[i] != "null") {
                node->left = new TreeNode(stoi(vec[i]));
                que.push(node->left);
            }
            i++;
            // 后创建右节点
            if (i < vec.size() && vec[i] != "null") {
                node->right = new TreeNode(stoi(vec[i]));
                que.push(node->right);
            }
            i++;
        }
        return root;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.deserialize(codec.serialize(root));

序列化，反序列化时间空间复杂度相同。其中 N 为可能的节点数。

时间复杂度： $O(N)$

空间复杂度：$O(N)$

剑指 Offer 38. 字符串的排列

Difficulty: 中等

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

1
2
输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

限制：

1 <= s 的长度 <= 8

Solution

方法一：常规回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 该方法遍历所有可能，最后在输入的时候通过再一次的查找重复项来去重，会超时 ！
// 该方法使用了记忆化，但是并没有用来去重，而是避免重复选择使用同一个位置元素而已
class Solution {
public:
    vector<string> res;
    string path;
    vector<string> permutation(string s) {
        vector<bool> visited(s.size(), false);
        backtracking(s, visited);
        return res;
    }
    void backtracking(string s, vector<bool>& visited) {
        if (path.size() == s.size()) {
            // 通过查找来判断是否存在重复项
            if (find(res.begin(), res.end()) == res.end()) {
                res.push_back();
            }
            return;
        }
        // 每次都遍历全部长度
        for (int i = 0; i < s.size(); i++) {
            if (visited[i]) continue;
            visited[i] = true;
            path += s[i];
            backtracking(s, visited);
            path.pop_back();
            visited[i] = false;
        }
    }
};

方法二：记忆化回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<string> res;
    string path;
    vector<string> permutation(string s) {
        // 需要提前排序
        sort(s.begin(), s.end());
        int len = s.size();
        vector<bool> visited(len);
        backtracking(s, visited);
        return res;
    }
    void backtracking(const string& s, vector<bool>& visited) {
        if (path.size() == s.size()) {
            res.push_back(path);
            return;
        }
        for (int i = 0; i < s.size(); i++) {
            // 关键在于同层去重，可以剪枝，具体详见备注
            if (i > 0 && s[i - 1] == s[i] && visited[i - 1] == false) continue;
            if (!visited[i]) {
                path += s[i];
                visited[i] = true;
                backtracking(s, visited);
                visited[i] = false;
                path.pop_back();
            }
        }
    }
};

备注 ：carl 大佬写的两篇相关文章，感受颇深！

去重思路：回溯算法：求组合总和（三）

树层上去重，与树枝上去重的区别：回溯算法：排列问题（二） (qq.com)

方法三：交换思想求取排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<string> permutation(string s) {
        dfs(s, 0);
        return res;
    }
private:
    vector<string> res;
    void dfs(string s, int x) {
        if(x == s.size() - 1) {
            res.push_back(s);                       // 添加排列方案
            return;
        }
        set<int> st;
        for(int i = x; i < s.size(); i++) {
            if(st.find(s[i]) != st.end()) continue; // 重复，因此剪枝
            st.insert(s[i]);
            swap(s[i], s[x]);                       // 交换，将 s[i] 固定在第 x 位
            dfs(s, x + 1);                          // 开启固定第 x + 1 位字符
            swap(s[i], s[x]);                       // 恢复交换
        }
    }
};

剑指 Offer 54. 二叉搜索树的第k大节点

Difficulty: 简单

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:

1
2
3
4
5
6
7
输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

示例 2:

1
2
3
4
5
6
7
8
9
输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

限制：

1 ≤ k ≤ 二叉搜索树元素个数

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        count = k;
        dfs(root);
        return res;
    }
    int res = 0, count = 0;
    // 二叉搜索树的中序遍历为递增序列，所以反向中序遍历可以获得递减序列
    void dfs(TreeNode* root) {
        if (!root) return;
        dfs(root->right);
        count--;
        if (!count) {
            res = root->val;
            return;
        }
        dfs(root->left);
    }
};

剑指 Offer 55 - I. 二叉树的深度

Difficulty: 简单

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最大深度 3 。

提示：

  1. 节点总数 <= 10000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

时间复杂度 ：$O(N)$， N 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度：$O(N)$， 最差情况下（当树退化为链表时），递归深度可达到 N 。

剑指 Offer 55 - II. 平衡二叉树

Difficulty: 简单

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

1
2
3
4
5
6
7
      1
     / \
    2   2
   / \
  3   3
 / \
4   4

返回 false 。

限制：

  • 0 <= 树的结点个数 <= 10000

Solution

方法一：先序遍历 + 判断深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if (!root) return true;
        return abs(dfs(root->left) - dfs(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
    int dfs(TreeNode* root) {
        if (!root) return 0;
        return max(dfs(root->left), dfs(root->right)) + 1;
    }
};

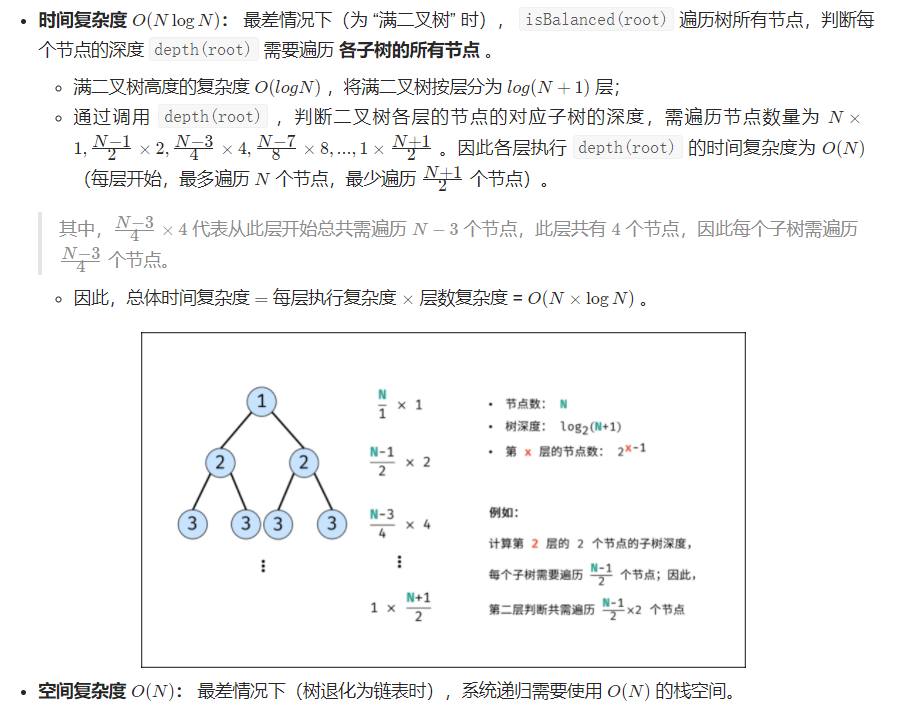
方法二：后序遍历 + 剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**

 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
 class Solution {
 public:
    bool isBalanced(TreeNode* root) {
        if (!root) return true;
        return getDep(root) != -1;
    }
    int getDep(TreeNode* root) {
        if (!root) return 0;
        int left = getDep(root->left);
        if (left == -1) return -1;
        int right = getDep(root->right);
        if (right == -1) return -1;
        if (abs(left - right) > 1) return -1;
        else return max(left, right) + 1;
    }
 };

时间复杂度 ：$O(N)$， N 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度：$O(N)$， 最差情况下（当树退化为链表时），递归深度可达到 N 。

剑指 Offer 64. 求1+2+…+n

Difficulty: 中等

求 1+2+...+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

示例 1：

1
2
输入: n = 3
输出: 6

示例 2：

1
2
输入: n = 9
输出: 45

限制：

  • 1 <= n <= 10000

Solution

1
2
3
4
5
6
7
8
class Solution {
public:
    int sumNums(int n) {
        // 利用门电路实现判断语句
        n > 1 && (n += sumNums(n - 1));
        return n;
    }
};

时间复杂度：$O(n) $， 计算 $n + (n-1) + … + 2 + 1n+(n−1)+…+2+1$ 需要开启 n 个递归函数。
空间复杂度： $O(n)$， 递归深度达到 n ，系统使用 $O(n)$ 大小的额外空间。

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

Difficulty: 简单

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

1
2
3
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

1
2
3
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。

Solution

方法一：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root || root == p || root == q) return root;
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        }
        else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};

时间复杂度： $O(N)$ ，其中 N 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为 $\log N$（满二叉树），最大为 N （退化为链表）。
空间复杂度： $O(N)$ ， 最差情况下，即树退化为链表时，递归深度达到树的层数 N 。

方法二：迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 提前比较p和q的大小，可以使得在循环中可减少判断条件，提升计算效率 
        if(p->val > q->val)
            swap(p, q);
        
        while(root != nullptr) {
            // p,q 都在 root 的右子树中
            // if(root->val < p->val && root->val < q->val) 
            
            if(root->val < p->val) // p,q 都在 root 的右子树中
                root = root->right; // 遍历至右子节点
            
            // p,q 都在 root 的左子树中
            // else if(root->val > p->val && root->val > q->val)
            
            else if(root->val > q->val) // p,q 都在 root 的左子树中
                root = root->left; // 遍历至左子节点
            else break;
        }
        return root;
    }
};

时间复杂度： $O(N)$ ，其中 N 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为 $\log N$（满二叉树），最大为 N （退化为链表）。
空间复杂度： $O(1)$ ，使用常数大小的额外空间。

剑指 Offer 68 - II. 二叉树的最近公共祖先

Difficulty: 简单

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

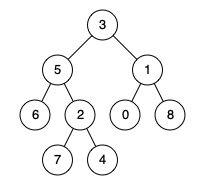
示例 1:

1
2
3
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

1
2
3
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉树中。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root || p == root || q == root) return root;

        TreeNode* left = lowestCommonAncestor(root->left, p , q);
        TreeNode* right = lowestCommonAncestor(root->right, p , q);

        if (!left) return right;
        else if (!right) return left;

        return root;
    }
};

时间复杂度 ：$O(N)$， N 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度：$O(N)$， 最差情况下（当树退化为链表时），递归深度可达到 N 。

参考资料

图解算法数据结构 - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台 (leetcode-cn.com)

#数据结构与算法 (qq.com)

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台 (leetcode-cn.com) 官方题解



----------- 本文结束 -----------




0%