剑指offer -- 数学

发表于 | 分类于
字数统计: 2.5k | 阅读时长 ≈ 11
安吉丽娜_朱莉

剑指offer – 数学

剑指 Offer 14- I. 剪绳子

Difficulty: 中等

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

1
2
3
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

  • 2 <= n <= 58

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int cuttingRope(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        
        // 为求最大乘积，需要尽可能的以 3 为分组
        int m = n % 3;
        int d = n / 3;

        // 可以分为 d 个 3
        if (!m) {
            return pow(3, d);
        }
        // 多出一个 1 
        else if (m == 1) {
            return pow(3, d - 1) * 4; 
        }
        // 多出一个 2 
        else {
            return pow(3, d) * 2;
        }
    }
};

剑指 Offer 14- II. 剪绳子 II

Difficulty: 中等

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

1
2
3
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

  • 2 <= n <= 1000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int cuttingRope(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        long res = 1;
        while (n > 4) {
            res *= 3;
            res %= 1000000007;
            n -= 3;
        }
        return int(res * n % 1000000007);

    }
};

剑指 offer 14 两道题基本相同，时间空间复杂度分析相同

时间复杂度： $O(1)$，简单的算术运算

空间复杂度： $O(1) $

剑指 Offer 39. 数组中出现次数超过一半的数字

Difficulty: 简单

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

1
2
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

限制：

1 <= 数组长度 <= 50000

Solution

方法一：排序

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0];
        sort(nums.begin(), nums.end());
        return nums[n / 2];
    }
};

取决于快速排序的时间空间复杂度

时间复杂度： $O(N \log N)$

空间复杂度： $O(\log N) $

方法二：哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int, int> mp;
        for (const auto& n : nums) {
            mp[n]++;
        }
        for (const auto& n : nums) {
            if (mp[n] >= (nums.size() + 1) / 2) {
                return n;
            }
        }
        return -1;
    }
};

时间复杂度： $O(N)$，简单的算术运算

空间复杂度： $O(N) $

方法二：摩尔投票

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0];
        int res = 0, count = 0;
        for (const auto& num : nums) {
            if (count == 0) {
                res = num;
                count++;
            } else {
                res == n ? count++ : count--;
            }
        }
        return res;
    }
};

时间复杂度： $O(N)$，简单的算术运算

空间复杂度： $O(1) $

剑指 Offer 43. 1～n 整数中 1 出现的次数

Difficulty: 困难

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

示例 1：

1
2
输入：n = 12
输出：5

示例 2：

1
2
输入：n = 13
输出：6

限制：

  • 1 <= n < 2^31

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int countDigitOne(int n) {
        long digit = 1;
        int high = n / 10;
        int cur = n % 10;
        int low = 0;
        int res;
        // 当 high 和 cur 同时为 0，说明已经越过最高位
        while (cur || high) {
            
            // 核心代码，3 个判断条件
            if (cur == 0) res += high * digit;
            else if (cur == 1) res += (high * digit) + low + 1;
            else res += (high + 1) * digit;
            
            // 将 cur 加入 low, 组成下轮 low, 也就是 low 左移
            low += cur * digit;
            // 下轮 cur 是本轮 high 的最低位, 也就是 cur 左移
            cur = high % 10;
            // 将本轮 high 最低位删除，得到下轮 high，也就是 high 左移
            high = high / 10;
            // 位因子每轮 * 10
            digit = digit * 10;
        }
    }
};

时间复杂度：$O(logn) $ ，循环内的计算操作使用 $O(1)$ 时间；循环次数为数字 n 的位数，即 $\log_{10}{n}$ ，因此循环使用 $O(\log n)$时间。
空间复杂度： $O(1)$， 几个变量使用常数大小的额外空间。

剑指 Offer 44. 数字序列中某一位的数字

Difficulty: 中等

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。

请写一个函数，求任意第n位对应的数字。

示例 1：

1
2
输入：n = 3
输出：3

示例 2：

1
2
输入：n = 11
输出：0

限制：

  • 0 <= n < 2^31

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) {
            n -= count;
            start *= 10;  // 1, 10, 100, ...
            digit += 1;   // 1, 2, 3, ...
            count = digit * start * 9; // 9, 180, 2700
        }
        // 确定num 
        long num = start + (n - 1) / digit;
        // 确定 n 位置在 num 中哪一位
        return to_string(num)[(n - 1) % digit] - '0';
    }
};

时间复杂度： $O(logn)$， 所求数位 n 对应数字 num 的位数 digit 最大为 $O(\log n)$ ；第一步最多循环 $O(\log n)$ 次；第三步中将 num 转化为字符串使用 $O(\log n)$ 时间；因此总体为 $O(\log n)$ 。
空间复杂度：$O(logn)$ ，将数字 num 转化为字符串 str(num) ，占用 $O(\log n)$ 的额外空间。

剑指 Offer 57 - II. 和为s的连续正数序列

Difficulty: 简单

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

示例 1：

1
2
输入：target = 9
输出：[[2,3,4],[4,5]]

示例 2：

1
2
输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

限制：

  • 1 <= target <= 10^5

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 双指针
class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        if (target == 1) return {};
        
        vector<vector<int>> res;
        int left = 1, right = 2;
        int sum = left + right;

        // 只需要循环到中位数即可
        while (right <= ((target + 1) / 2)) {
            while (left < right) {     
                if (target == sum) {
                    vector<int> temp;
                    for (int i = left; i <= right; i++) {
                        temp.push_back(i);
                    }
                    res.push_back(temp);
                    sum -= left;
                    left++;
                } else if (target < sum) {
                    sum -= left;
                    left++;
                } else {
                    right++;
                    sum += right;
                }
            }
            right++; // 跳出中位数
        }
        return res;
    }
};

时间复杂度： $O(N)$，其中 $N = target$；连续整数序列至少有两个数字，而 $i < j$恒成立，因此至多循环 $target$ 次（ $i , j$ 都移动到 $\frac{target}{2}$ ），使用 $O(N)$ 时间；当 $i = 1$ 时，达到最大序列长度 $\frac{-1 + \sqrt{1 + 8s}}{2}$ ，考虑到解的稀疏性，将列表构建时间简化考虑为 $O(1)$；

空间复杂度： $O(1) $

剑指 Offer 62. 圆圈中最后剩下的数字

Difficulty: 简单

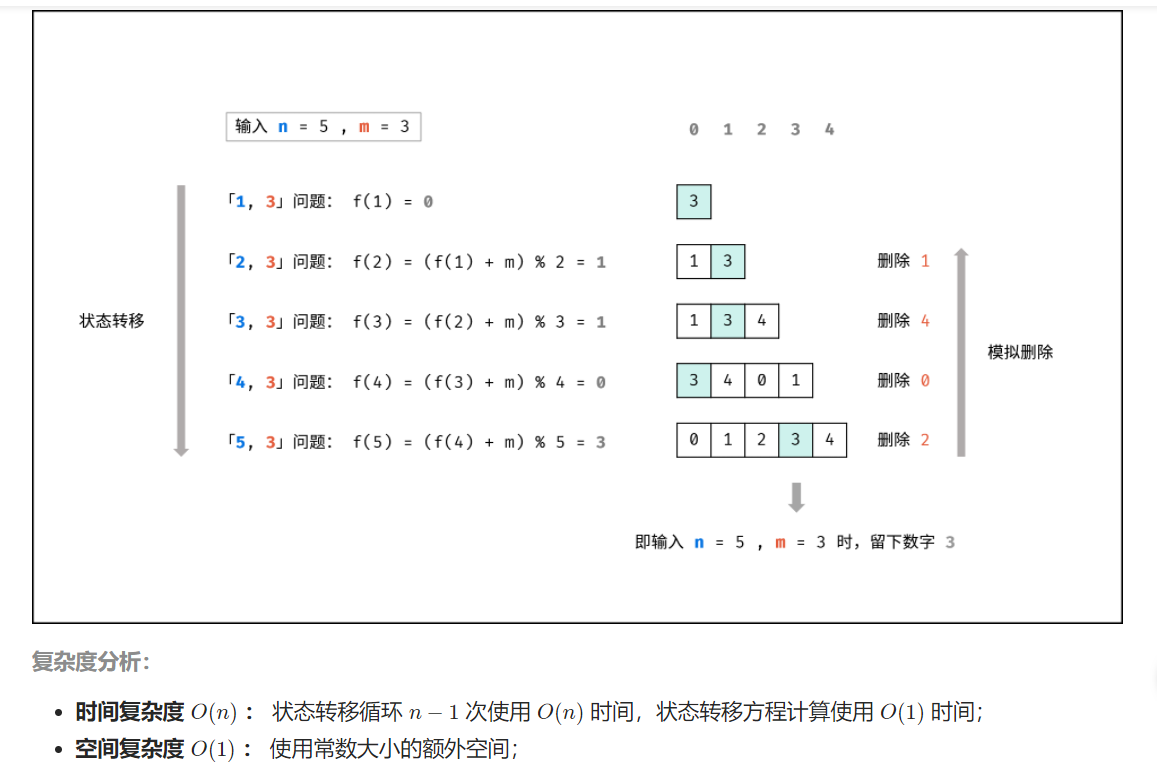
0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

1
2
输入: n = 5, m = 3
输出: 3

示例 2：

1
2
输入: n = 10, m = 17
输出: 2

限制：

  • 1 <= n <= 10^5
  • 1 <= m <= 10^6

Solution

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int lastRemaining(int n, int m) {
        int res = 0;
        for (int i = 2; i <= n; i++) {
            res = (res + m) % i;
        }
        return res;
    }
};

剑指 Offer 66. 构建乘积数组

Difficulty: 中等

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

示例:

1
2
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

提示：

  • 所有元素乘积之和不会溢出 32 位整数
  • a.length <= 100000

Solution

方法一：当前位置的值 = 左边乘积 * 右边乘积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> constructArr(vector<int>& a) {
        int n = a.size();

        // 设定动态规划矩阵
        vector<int> dpLeft(n + 1, 1);
        vector<int> dpRight(n + 1, 1);
		
        // 简单求取左右乘积矩阵
        for (int i = 1, j = n - 1; i < n, j >= 0; i++, j--){
            dpLeft[i] = dpLeft[i - 1] * a[i - 1];
            dpRight[j] = dpRight[j + 1] * a[j];
        }
        vector<int> res(n);
        for (int i = 0; i < n; i++) {
            res[i] = dpLeft[i] * dpRight[i + 1];
        }
        return res;  
    }
};

时间复杂度： $O(N)$，2次遍历数组

空间复杂度： $O(N) $，左右乘积矩阵占用的空间

方法二：双向遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> constructArr(vector<int>& a) {
        int n = a.size();
		vector<int> B(n);
        int temp = 1;
        // 正向遍历,获得左乘积矩阵
        for (int i = 0; i < n; i++) {
            B[i] = temp;
            temp *= a[i];
        }
        temp = 1;
        // 反向遍历,获得右乘积矩阵，同时与左乘积矩阵相乘，相比于方法一少去一部分操作
        for (int i = n - 1; i >= 0; i--) {
            B[i] = B[i] * temp;
            temp *= a[i];
        }
        return B;
    }
};

时间复杂度： $O(N)$，2次遍历数组

空间复杂度： $O(N) $，数组 B 占用的空间

参考资料

图解算法数据结构 - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台 (leetcode-cn.com)

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台 (leetcode-cn.com) 官方题解



----------- 本文结束 -----------




0%