剑指offer -- 数据结构

发表于 | 分类于
字数统计: 5.9k | 阅读时长 ≈ 27
埃菲尔铁塔 -- 法国

剑指offer – 数据结构

剑指 Offer 05. 替换空格

Difficulty: 简单

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例 1：

1
2
输入：s = "We are happy."
输出："We%20are%20happy."

限制：

0 <= s 的长度 <= 10000

Solution

方法一：正序修改

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    string replaceSpace(string s) {
        string res;
        for (int i = 0; i < s.length(); i++) {
            if (s[i] == ' ') {
                res += "%20";
            }
            else res += s[i];
        }
        return res;
    }
};

时间复杂度：$O(N)$，N 为 s 的长度。

空间复杂度：$O(N)$，res 所需要的额外空间。

方法二：反向修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    string replaceSpace(string s) {
        int len = s.size();
        int count = 0;
        // 统计空格的数量
        for (const auto& a : s) {
            if (a == ' ') count++;
        }
        s.resize(len + 2 * count); // 修改 s 的长度
        // 双指针倒序
        for (int i = len - 1, j = s.size() - 1; i < j; i--, j--) {
            if (s[i] != ' ') {
                s[j] = s[i];
            } else {
                s[j] = '0';
                s[j - 1] = '2';
                s[j - 2] = '%';
                j -= 2;
            }
        }
        return s;
    }
};

时间复杂度：$O(N)$，N 为 s 的长度。

空间复杂度：$O(1)$，由于原地扩展 s 的长度，因此使用常数的额外空间。

剑指 Offer 06. 从尾到头打印链表

Difficulty: 简单

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例 1：

1
2
输入：head = [1,3,2]
输出：[2,3,1]

限制：

0 <= 链表长度 <= 10000

Solution

方法一：正序输入，反转数组

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int> res;
        while (head) {
            res.push_back(head->val);
            head = head->next;
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

时间复杂度：$O(N)$，N 为链表长度，一次遍历链表。

空间复杂度：$O(N)$，res 所需要的额外空间。

方法二：辅助栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        stack<int> stk;
        while(head != nullptr) {
            stk.push(head->val);
            head = head->next;
        }
        vector<int> res;
        while(!stk.empty()) {
            res.push_back(stk.top());
            stk.pop();
        }
        return res;
    }
};

时间复杂度：$O(N)$，N 为链表长度，一次遍历链表。

空间复杂度：$O(N)$，stk 所需要的额外空间。

方法三：递归

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        if(!head)
            return {};
        // 递归在 push 之前
        vector<int> a = reversePrint(head->next);
        a.push_back(head->val); 
        return a;
    }
};

时间复杂度：$O(N)$，N 为链表长度，一次遍历链表。

空间复杂度：$O(N)$，系统递归所需要使用的栈空间。

剑指 Offer 09. 用两个栈实现队列

Difficulty: 简单

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

1
2
3
4
输入：
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出：[null,null,3,-1]

示例 2：

1
2
3
4
输入：
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出：[null,-1,null,null,5,2]

提示：

  • 1 <= values <= 10000
  • 最多会对 appendTail、deleteHead 进行 10000 次调用

Solution

方法一：每次delete，都进行倒出倒入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class CQueue {
public:
    stack<int> stack1;
    stack<int> stack2;
    CQueue() {
    }  
    void appendTail(int value) {
        // 1 压栈
        stack1.push(value);
    } 
    int deleteHead() {
        //  1 空 则返回 - 1
        if (stack1.empty()) return -1;
        // 将 1 中元素倒入 2
        while (!stack1.empty()) {
            int temp = stack1.top();
            stack1.pop();
            stack2.push(temp);
        }
        // 记录 2 中栈顶元素为结果
        int res = stack2.top();
        stack2.pop();
        // 倒回去
        while (!stack2.empty()) {
            int temp = stack2.top();
            stack2.pop();
            stack1.push(temp);
        }
        return res;
    }
};

**时间复杂度：**插入操作 $O(1)$，删除操作 $O(N)$

空间复杂度：$O(N)$

方法二：仅输出栈空调用倒入操作，无倒回操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class CQueue {
public:
    stack<int> stack1; // 输入栈
    stack<int> stack2; // 输出栈
    CQueue() {
    }  
    void appendTail(int value) {
        // 压栈
        stack1.push(value);
    } 
    int deleteHead() {
        // 如果输出栈为空，则需要倒入输入栈的数据
        if (stack2.empty()) {
            while (!stack1.empty()) {
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        // 如果此时仍然为空，则说明没有元素，返回-1
        if (stack2.empty()) return -1;
        // 否则，弹出输出栈栈顶元素即可
        else {
            int deleteItem = stack2.top();
            stack2.pop();
            return deleteItem;
        }    
    }
};

**时间复杂度：**插入操作 $O(1)$，删除操作 $O(N)$

空间复杂度：$O(N)$

剑指 Offer 20. 表示数值的字符串

Difficulty: 中等

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

数值（按顺序）可以分成以下几个部分：

  1. 若干空格
  2. 一个 小数 或者 整数
  3. （可选）一个 'e' 或 'E' ，后面跟着一个 整数
  4. 若干空格

小数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（'+' 或 '-'）
  2. 下述格式之一：
    1. 至少一位数字，后面跟着一个点 '.'
    2. 至少一位数字，后面跟着一个点 '.' ，后面再跟着至少一位数字
    3. 一个点 '.' ，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（'+' 或 '-'）
  2. 至少一位数字

部分数值列举如下：

  • ["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]

部分非数值列举如下：

  • ["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]

示例 1：

1
2
输入：s = "0"
输出：true

示例 2：

1
2
输入：s = "e"
输出：false

示例 3：

1
2
输入：s = "."
输出：false

示例 4：

1
2
输入：s = "    .1  "
输出：true

提示：

  • 1 <= s.length <= 20
  • s 仅含英文字母（大写和小写），数字（0-9），加号 '+' ，减号 '-' ，空格 ' ' 或者点 '.' 。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    bool isNumber(string s) {
        unordered_map<int, unordered_map<char, int>> mp {
            { 0, { {' ', 0}, {'s', 1}, {'d', 2}, {'.', 4} } },
            { 1, { {'d', 2}, {'.', 4} } },
            { 2, { {'d', 2}, {'.', 3}, {'e', 5}, {' ', 8} } },
            { 3, { {'d', 3}, {'e', 5}, {' ', 8} } },
            { 4, { {'d', 3} } },
            { 5, { {'s', 6}, {'d', 7} } },
            { 6, { {'d', 7} } },
            { 7, { {'d', 7}, {' ', 8} } },
            { 8, { {' ', 8} } }
        };
        int state = 0;
        char t;
        for (const auto c : s) {
            if (isdigit(c)) t = 'd';
            else if (c == '+' || c == '-') t = 's';
            else if (c == '.' || c == ' ') t = c;
            else if (c == 'e' || c == 'E') t = 'e';
            else t = '?'; // 当前输入有问题，之后在 mp 中一定找不到，会直接返回 false
            // 如果在当前状态转化表中没有找到当前 key
 			// 则说明正常情况下该状态不期待出现该输入
            if (!mp[state].count(t)) return false; 
            state = mp[state][t];  // 状态转移
        }
        // 只有 2 3 7 8 四种状态是合法的退出状态
        return state == 2 || state == 3 || state == 7 || state == 8;
    }
};

时间复杂度： $O(N)$，其中 N 为字符串 s 的长度，一次遍历即可。

空间复杂度：$O(1)$，mp 和 state 使用常数大小的额外空间。

状态转移图见：

图解算法数据结构_剑指offer20

剑指 Offer 24. 反转链表

Difficulty: 简单

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

1
2
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

限制：

0 <= 节点个数 <= 5000

Solution

方法一：双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* post = cur->next;
            cur->next = pre;
            pre = cur;
            cur = post;
        }
        return pre;
    }
};

时间复杂度：$O(N)$，N 为链表长度，一次遍历链表。

空间复杂度：$O(1)$，pre, cur, post 所需要常数级的额外空间。

方法二：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        return recur(head, nullptr);           // 调用递归并返回
    }
private:
    ListNode* recur(ListNode* cur, ListNode* pre) {
        if (cur == nullptr) return pre;        // 终止条件
        ListNode* res = recur(cur->next, cur); // 递归后继节点
        cur->next = pre;                       // 修改节点引用指向
        return res;                            // 返回反转链表的头节点
    }
};

时间复杂度：$O(N)$，N 为链表长度，一次遍历链表。

空间复杂度：$O(N)$，遍历链表的递归深度达到 N，系统使用 O(N) 大小的额外空间。

剑指 Offer 30. 包含min函数的栈

Difficulty: 简单

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

1
2
3
4
5
6
7
8
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

提示：

  1. 各函数的调用总次数不超过 20000 次

Solution

方法一：vector 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class MinStack {
public:
    /** initialize your data structure here. */
    vector<int> stack;
    vector<int> minN;
    MinStack() {
        minN.push_back(INT_MAX);
    }
    void push(int x) {
        stack.push_back(x);
        // 输入的x更小
        if (minN.back() > x) {
            minN.push_back(x);
        } else { // 该步骤不能省略
            minN.push_back(minN.back());
        }
    }
    void pop() {
        minN.pop_back();
        stack.pop_back();
    }
    int top() {
        return stack.back();
    }
    int min() {
        if (stack.empty()) return -1;
        else return minN.back();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->min();
 */

方法二：stack 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class MinStack {
public:
    /** initialize your data structure here. */
    stack <int> s;
    stack <int> m;
    MinStack() {
    }
    void push(int x) {
        s.push(x);
        if(m.empty() || x <= m.top()) m.push(x);
    }
    void pop() {
        if(s.top() == m.top())  m.pop();
        s.pop();
    }
    int top() {
        return s.top();
    }
    int min() {
        return m.top();
    }
};

时间复杂度：$O(1)$，push, pop, top, min，皆是 $O(1)$。

空间复杂度：$O(N)$，需要额外的 vector 空间，或者 stack 空间。

剑指 Offer 35. 复杂链表的复制

Difficulty: 中等

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 1：

1
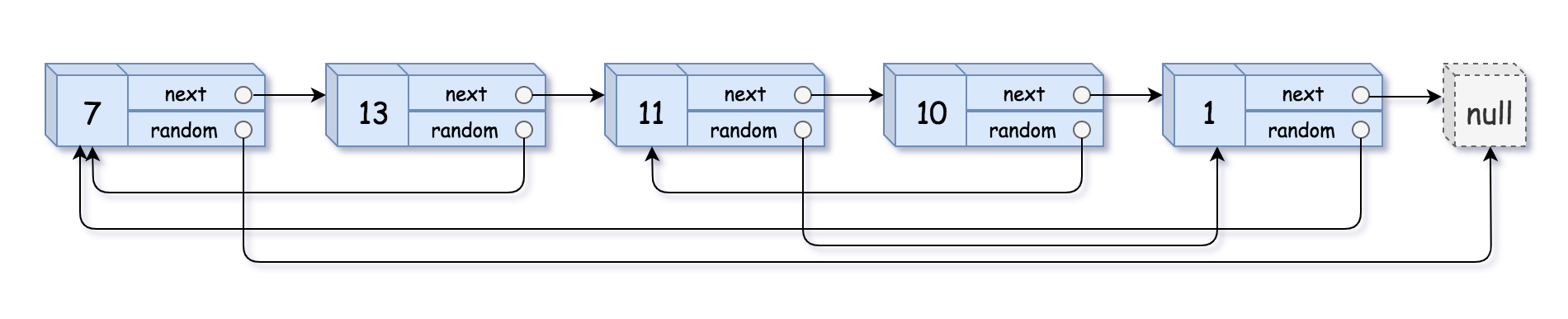
2
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

1
2
输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

1
2
输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

示例 4：

1
2
3
输入：head = []
输出：[]
解释：给定的链表为空（空指针），因此返回 null。

提示：

  • -10000 <= Node.val <= 10000
  • Node.random 为空（null）或指向链表中的节点。
  • 节点数目不超过 1000 。

Solution

方法一：哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr) return nullptr;
        Node* cur = head;
        unordered_map<Node*, Node*> map;
        // 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
        while(cur != nullptr) {
            map[cur] = new Node(cur->val);
            cur = cur->next;
        }
        cur = head;
        // 4. 构建新链表的 next 和 random 指向
        while(cur != nullptr) {
            map[cur]->next = map[cur->next];
            map[cur]->random = map[cur->random];
            cur = cur->next;
        }
        // 5. 返回新链表的头节点
        return map[head];
    }
};

时间复杂度：$O(N)$，N 为链表长度，两次遍历链表。

空间复杂度：$O(N)$，哈希表所需的额外空间。

方法二：拼接 + 拆分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr) return nullptr;
        Node* cur = head;
        // 1. 复制各节点，并构建拼接链表
        while(cur != nullptr) {
            Node* tmp = new Node(cur->val);
            tmp->next = cur->next;
            cur->next = tmp;
            cur = tmp->next;
        }
        // 2. 构建各新节点的 random 指向
        cur = head;
        while(cur != nullptr) {
            if(cur->random != nullptr)
                cur->next->random = cur->random->next;
            cur = cur->next->next;
        }
        // 3. 拆分两链表
        cur = head->next;
        Node* pre = head, *res = head->next;
        while(cur->next != nullptr) {
            pre->next = pre->next->next;
            cur->next = cur->next->next;
            pre = pre->next;
            cur = cur->next;
        }
        pre->next = nullptr; // 单独处理原链表尾节点
        return res;      // 返回新链表头节点
    }
};

时间复杂度：$O(N)$，N 为链表长度，三次遍历链表。

空间复杂度：$O(1)$，节点引用变量所需的额外空间。

剑指 Offer 58 - II. 左旋转字符串

Difficulty: 简单

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。

示例 1：

1
2
输入: s = "abcdefg", k = 2
输出: "cdefgab"

示例 2：

1
2
输入: s = "lrloseumgh", k = 6
输出: "umghlrlose"

限制：

  • 1 <= k < s.length <= 10000

Solution

1
2
3
4
5
6
7
8
9
class Solution {
public:
    string reverseLeftWords(string s, int n) {
        reverse(s.begin(), s.begin() + n);
        reverse(s.begin() + n, s.end());
        reverse(s.begin(), s.end());
        return s;
    }
};

时间复杂度：$O(N)$，N 为 s 的长度，共两次遍历 s。

空间复杂度：$O(1)$，C++ 原地字符串操作，使用常数大小额外空间。

剑指 Offer 59 - I. 滑动窗口的最大值

Difficulty: 困难

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

提示：

你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

Solution

方法一：优先队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        priority_queue<pair<int, int>> q;
        for (int i = 0; i < k; ++i) {
            q.emplace(nums[i], i);
        }
        vector<int> ans = {q.top().first};
        for (int i = k; i < n; ++i) {
            q.emplace(nums[i], i);
            while (q.top().second <= i - k) {
                q.pop();
            }
            ans.push_back(q.top().first);
        }
        return ans;
    }
};

时间复杂度：$O(N\log N)$，其中 N 是 nums 的长度，nums 单调递增情况，优先队列包含所有元素，没有元素被移除，下一个元素放入优先队列的时间复杂度为 $O(\log N)$，因此总的时间复杂度为 $O(n \log N)$。

空间复杂度：$O(N)$，nums 单调递增情况下会存下所有元素。

方法二：单调队列（存元素）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        if (n == 0) return {};
        deque<int> q;
        // 处理 前 k 个
        for (int i = 0; i < k; i++) {
            // push 操作
            // 单调队列写法，队首元素总是最大值
            while (!q.empty() && nums[i] > q.back()) {
                q.pop_back();
            }
            q.push_back(nums[i]);
        }
        vector<int> res;
        res.push_back(q.front());
        // 处理后 n - k 个
        for (int i = k; i < n; i++) {
            // 关键，需要在 push 之前判断，以当前位置为右边框，左边框元素是否在队列中
            // 如果在队列中，需要 pop 它
            // push 操作
            if (q.front() == nums[i - k]) q.pop_front();
            while (!q.empty() && nums[i] > q.back()) {
                q.pop_back();
            }
            q.push_back(nums[i]);
            // 记录结果
            res.push_back(q.front());
        }
        return res;
    }
};

方法三：单调队列（存元素索引）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        if (n == 0) return {};
        deque<int> q;
        for (int i = 0; i < k; ++i) {
            while (!q.empty() && nums[i] >= nums[q.back()]) {
                q.pop_back();
            }
            // 与方法一相似，只不过此时存入队列的是元素索引
            q.push_back(i);
        }
        vector<int> res = {nums[q.front()]};
        for (int i = k; i < n; ++i) {
            while (!q.empty() && nums[i] >= nums[q.back()]) {
                q.pop_back();
            }
            q.push_back(i);
            // 同样要判断，以当前位置为右边框，左边框元素是否在队列中
            // 如果在队列中，需要 pop 它
            while (q.front() <= i - k) {
                q.pop_front();
            }
            res.push_back(nums[q.front()]);
        }
        return res;
    }
};

两种方法的时间空间复杂度相同。

时间复杂度：$O(N)$，其中 N 是 nums 的长度，每个位置的元素或者索引恰好被放入队列一次，并且最多被弹出队列一次。

空间复杂度：$O(K)$，超出 K，会有 pop 操作，所以队列中的元素个数不会超过 K；

剑指 Offer 59 - II. 队列的最大值

Difficulty: 中等

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1：

1
2
3
4
输入: 
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

示例 2：

1
2
3
4
输入: 
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出: [null,-1,-1]

限制：

  • 1 <= push_back,pop_front,max_value的总操作数 <= 10000
  • 1 <= value <= 10^5

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class MaxQueue {
public:
    deque<int> maxQ;  // 用来存队列最大值, 越靠近队首元素越大
    queue<int> que;   // 队列
    MaxQueue() {}

    int max_value() {
        // 队列为空，直接返回 -1
        if (que.size()== 0) {
            return -1;
        }
        // 否则反馈 最大值队列队首
        return maxQ.front();
    }

    void push_back(int value) {
        que.push(value);  // 队列 push
        // 如果最大值队列为空，当前值就是最大值，直接push到最大值队列
        if (maxQ.size() == 0) {
            maxQ.push_back(value);
        }
        // 当前值大于队首，也就是大于所有值，直接清空最大值队列并push当前值 
        else if (value > maxQ.front()) {
            maxQ.clear();
            maxQ.push_back(value);
        }
        // 否则pop掉比它小的的，放入该放入的位置 
        else {
            while (maxQ.back() < value) {
                maxQ.pop_back();
            }
            maxQ.push_back(value);
        }
    }

    int pop_front() {
        if (que.size() == 0) return -1;
        int res = que.front();
        que.pop();
        // 如果 push 的是最大值，需要将 maxQ 队首 pop
        if (res == maxQ.front()) maxQ.pop_front();
        return res;
    }
};

/**
 * Your MaxQueue object will be instantiated and called as such:
 * MaxQueue* obj = new MaxQueue();
 * int param_1 = obj->max_value();
 * obj->push_back(value);
 * int param_3 = obj->pop_front();
 */

时间复杂度：$O(1)$，max_value(), push_back()，pop_front() 方法的均摊时间复杂度均为 $O(1)$

空间复杂度：$O(N)$，如果连续存入递增序列，maxQ 中存 N 个元素，使用 $O(N)$ 的额外空间。

剑指 Offer 67. 把字符串转换成整数

Difficulty: 中等

写一个函数 StrToInt，实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例 1:

1
2
输入: "42"
输出: 42

示例 2:

1
2
3
4
输入: "   -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
     我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

1
2
3
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ，因为它的下一个字符不为数字。

示例 4:

1
2
3
4
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
     因此无法执行有效的转换。

示例 5:

1
2
3
4
输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。 
     因此返回 INT_MIN (−231) 。

Solution

方法一：遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    int strToInt(string str) {
        // INT_MIN ~ MAX [-2147483648, 2147483647 ] 
        // 一：(2147483647 / 10) * 10 = 2147483650 > INT_MAX 越界
        // 二：2147483648 ~ 2147483649 越界 

        int res = 0, bound = INT_MAX / 10; 
        int i = 0, sign = 1, len = str.size();
        if (len == 0) return 0;
        // 去最前方空格
        while (str[i] == ' ') {
            // 如果整个字符串全空格，则返回 0
            if (++i == len) return 0;
        }
        // 判断 + - 号
        if (str[i] == '-') {
            sign = -1;
            i++;
        } else if (str[i] == '+') {
            i++;
        }
        
        for (int j = i; j < len; j++) {
            // 如果不是数字，直接 break
            if (str[j] > '9' || str[j] < '0') break;
            // 如果越界
            if (res > bound || (res == bound && str[j] > '7')) {
                // 看符号判断越上界还是下界
                return sign == 1 ? INT_MAX : INT_MIN;
            }
            // 10 进制更新
            res = res * 10 + (str[j] - '0');
        }
        return sign * res;
    }
};

时间复杂度：$O(N)$，其中 N 为字符串长度，遍历字符串；

空间复杂度：$O(N)$，删除首尾空格后需要建立新字符串，最差情况下占用 $O(N)$ 额外空间。

注意：该方法的越界判断十分巧妙！

图解算法数据结构_剑指offer67

方法二：先找数字首位，本质相同，只不过通过 STL 算法来实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
public:
    // 注意：使用的 leetcode 8 “字符串转整数”，那个题目的变量名称。
    int myAtoi(string s) {
        // 利用 STL 算法 find_first_of() 来找到字符串中第一个数字出现的位置，确定开头位置。
        size_t pos = s.find_first_of("0123456789");
        if (pos == -1) return 0; // 没有找到，说明这个字符串里面一个数字都没有，直接返回 0
        // 在字符串首部就找到，也就是字符串第一个符号就是数字
        else if (pos == 0) {
            string temp = "";
            int i = pos; // i = 0;
            while (i < s.size()) { // 往后遍历，确定数字
                if (isdigit(s[i])) {
                    temp += s[i++];
                } else break;
            }
            long long res = 0;
            stringstream ss;  // 通过 stringstream 函数 可以将 string 转化为 long long
            ss << temp;
            ss >> res;
            // 判断上下限
            if (res > INT_MAX) return INT_MAX;
            else if (res < INT_MIN) return INT_MIN;
            else return int(res);   
        }
        // 非首部找到，需要判断前面的几种情况 
        else {
            // 此时需要判断，数字之前有没有出现空格以外的符号
            // 注意此时 i < pos - 1, 需要留下数字前一位置，它可能是符号位，单独判断
            for (int i = 0; i < pos - 1; i++) {
                if (!isspace(s[i])) return 0;  // 存在其他符号，直接返回 0
            }
            // 单独判断数字前一位
            if (!(s[pos - 1] == ' ' || s[pos - 1] == '-' || s[pos - 1] == '+')) {
                return 0;
            } 
            // 同上文处理
            string temp = "";
            int i = pos;
            while (i < s.size()) {
                if (isdigit(s[i])) {
                    temp += s[i++];
                } else break;
            }
            long long res = 0;
            stringstream ss;
            ss << temp;
            ss >> res;
            // 要先处理正负号问题，在进行大小值判断
            if (s[pos - 1] == '-') res = -res;
            if (res > INT_MAX) return INT_MAX;
            else if (res < INT_MIN) return INT_MIN;
            else return int(res); 
        }
    }
};

时间复杂度：$O(N)$，其中 N 为字符串长度，遍历字符串；

空间复杂度：$O(N)$，中间变量 temp, stringstream 对象等所需的额外空间。

参考资料

图解算法数据结构 - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台 (leetcode-cn.com)

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台 (leetcode-cn.com) 官方题解



----------- 本文结束 -----------




0%